위로 아래

트리 데이터 구조

특징

  1. 비선형 자료 구조.
  2. 계층적 관계를 표현하는 자료 구조.
  3. 트리는 하나 이상의 루트 노드를 갖는다.
  4. 루트 노드는 0개 이상의 자식 노드를 갖는다.
  5. 사이클이 존재할 수 없다.
  6. self-loop가 존재할 수 없다.
  7. 키-값 유형 구조 : 노드에 저장된 데이터를 식별하는데 사용되는 키(key)와 노드에 저장된 데이터 값(value) 사이의 관계 구조
  8. 순회(traversal) : 트리를 탐색하는 과정

 

구성

  1. 루트 노드(root node) : 트리 데이터 구조의 맨 위에 해당하는 노드.
  2. 자식 노드(child node), 하위 노드 : 루트 노드에서 멀어지는 방향으로 연결된 노드. 부모 노드는 여러 개의 자식 노드를 가질 수 있다.
  3. 부모 노드(parent node), 상위 노드 : 루트 노드 방향으로 연결된 노드. 자식 노드는 부모 노드를 한 개만 가질 수 있다.
  4. 리프 노드(leaf node), 말단 노드 : 더이상 자식 노드를 갖지 않는 트리의 마지막 노드.
  5. 에지(edge) : 트리에서 노드를 연결하는 선
  6. 서브트리(subtree), 하위 트리 : 하나의 노드와 그 자식 노드들로 구성된 작은 트리 구조.

 

이진 탐색 트리

이진 트리(binary tree)

자식 노드가 최대 2개인 노드가 모여서 형성된 트리 구조.

 

 

 

이진 탐색 트리(binary search tree)

  1. 특징
    1. 노드의 키를 기준으로 정렬한 이진 트리.
    2. 모든 노드의 키는 왼쪽 서브트리보다 크고 오른쪽 서브트리보다 작다.
    3. 최대 트리의 높이 h -> 시간 복잡도 O(h)
    4. 가장 작은 키를 갖는 노드 : 최상위 노드에서 가장 왼쪽에 있는 서브트리의 말단에 위치
    5. 가장 큰 키를 갖는 노드 : 최상위 노드에서 가장 오른쪽에 있는 서브트리의 말단에 위치
  2. 동작
    1. 트리에 노드를 추가
    2. 트리에서 노드를 삭제
    3. 노드를 선택해 탐색하고자 하는 키가 존재하는지 확인
  3. 탐색 과정
    1. 찾고자 하는 값 > 루트 노드의 값 -> 오른쪽 서브트리로 탐색 진행 
    2. 찾고자 하는 값 < 루트 노드의 값 -> 왼쪽 서브트리로 탐색 진행

 

불균형 트리

불균형 트리

  1. 특징
    1. 많은 노드가 단 하나의 자식 노드만을 갖는 구조
    2. 트리의 불균형을 해결하는 것은 메모리 관리를 위해 중요하다. 균형잡힌 트리가 메모리를 더 효율적으로 이용한다.
    3. 균형을 조절하려면, 트리의 역할을 유지하되 가능한 트리의 높이를 최소로 만들어야 한다. 

 

트리 회전

서브트리 2개 사이에서 높은 차이를 감지하면 균형 조정 과정을 수행한다.

 

이진 탐색 트리 : AVL 트리

AVL 트리 (Adelson-Velsky and Landis tree)

  1. 트리 회전(tree rotation)을 통해 자체적으로 균형을 조정하는 트리.
  2. 일부 데이터베이스 검색 시스템에서 사용된다.
  3. 시간 복잡도 O(logn)

 

이진 탐색 트리 : RB 트리

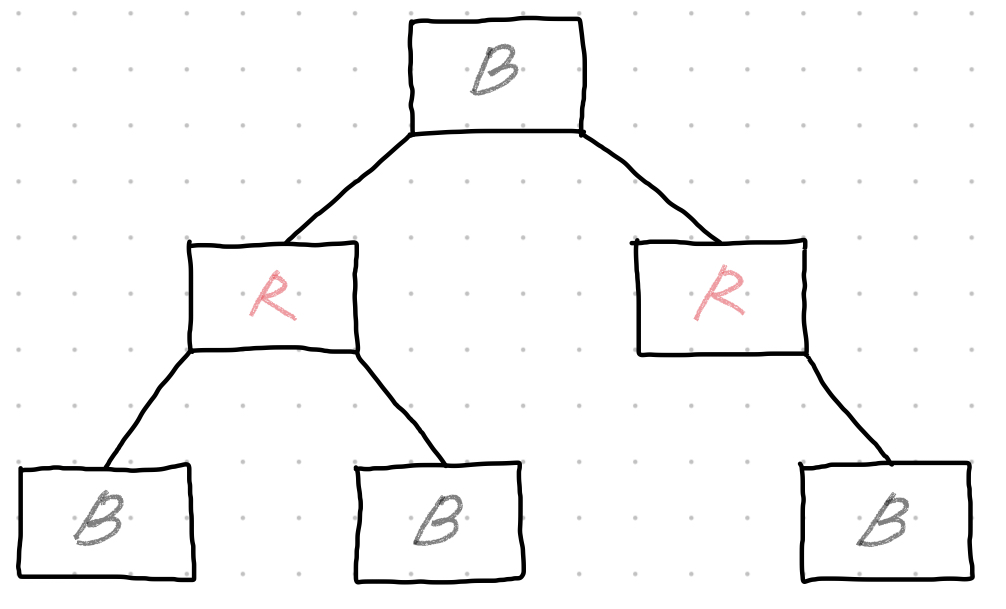
RB 트리 (Red-Black tree)

  1. 트리 회전(tree rotation)을 통해 자체적으로 균형을 조정하는 트리.
  2. 트리 균형을 조정하는 과정에서 트리 회전 수가 적어 AVL 트리보다 효율적이다.
  3. 노드마다 red, black으로 해석되는 비트를 포함하며, root node는 black을 지니고, red node는 child node로 black node를 가진다. 
  4. 시간 복잡도 O(logn)

이진 탐색 트리 : B 트리

B 트리 

  1. 3개 이상의 자식 노드를 가질 수 있다.
  2. 데이터베이스 시스템을 설계할 때 사용하는 데이터 구조.
  3. 트리 회전(tree rotation)을 통해 자체적으로 균형을 조정하는 트리.
  4. 파일 시스템에서 쓰인다. 노드의 키-값 구조를 통해 여러 파일이 들어있는 폴더를 포함하고 있는 폴더의 이름과 파일 시스템의 객체를 연결하는 구조에 적합하다.

 

이진 탐색 트리 : 힙

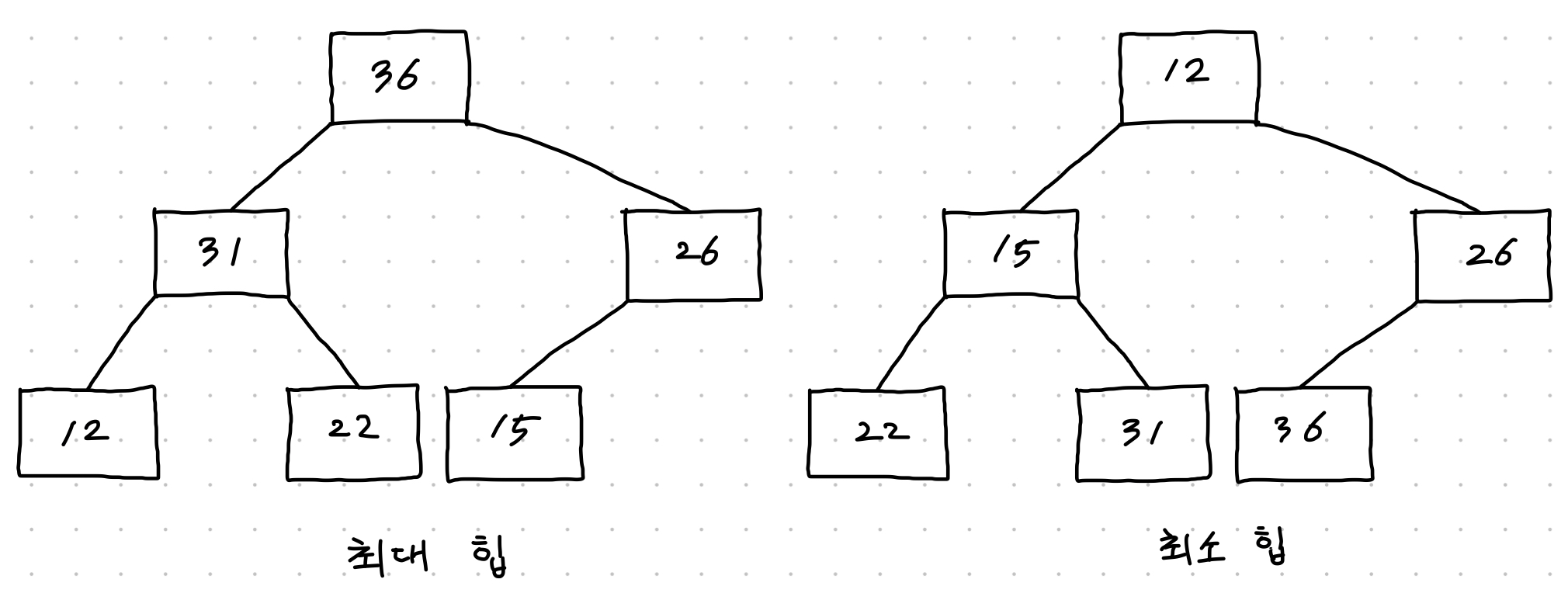
힙

  1. 값이 최대 혹은 최소인 노드에 빠르게 접근해야하는 응용 프로그램에 적합하다.
  2. 힙 메모리 : 프로그래머가 직접 관리해야 하는 메모리의 영역. 프로그래머가 작성한 코드에 따라 메모리 공간을 동적으로 할당하거나 해제하는 부분이기도 하다.
  3. 힙 데이터 구조는 힙 메모리와 전혀 다른 개념이다.
  4. 힙의 구조를 설계하는 방법
    1. 최대 힙(max heap) : 루트 노드가 힙에서 가장 큰 값이고, 노드 각각의 값이 부모 노드의 값보다 작거나 같도록 구성된 힙.
    2. 최소 힙(min heap) : 루트 노드가 힙에서 가장 작은 값이고 노드 각각의 값이 부모 노드의 값보다 크거나 같도록 구성된 힙. 
     

저작자표시

티스토리툴바